Open
Description
虽然这是一道难度为困难的题,不过大家不要被它所迷惑,其实它不是很难。
解决这道题,最直观的办法就是暴力求解。我们可以先来分析一波:
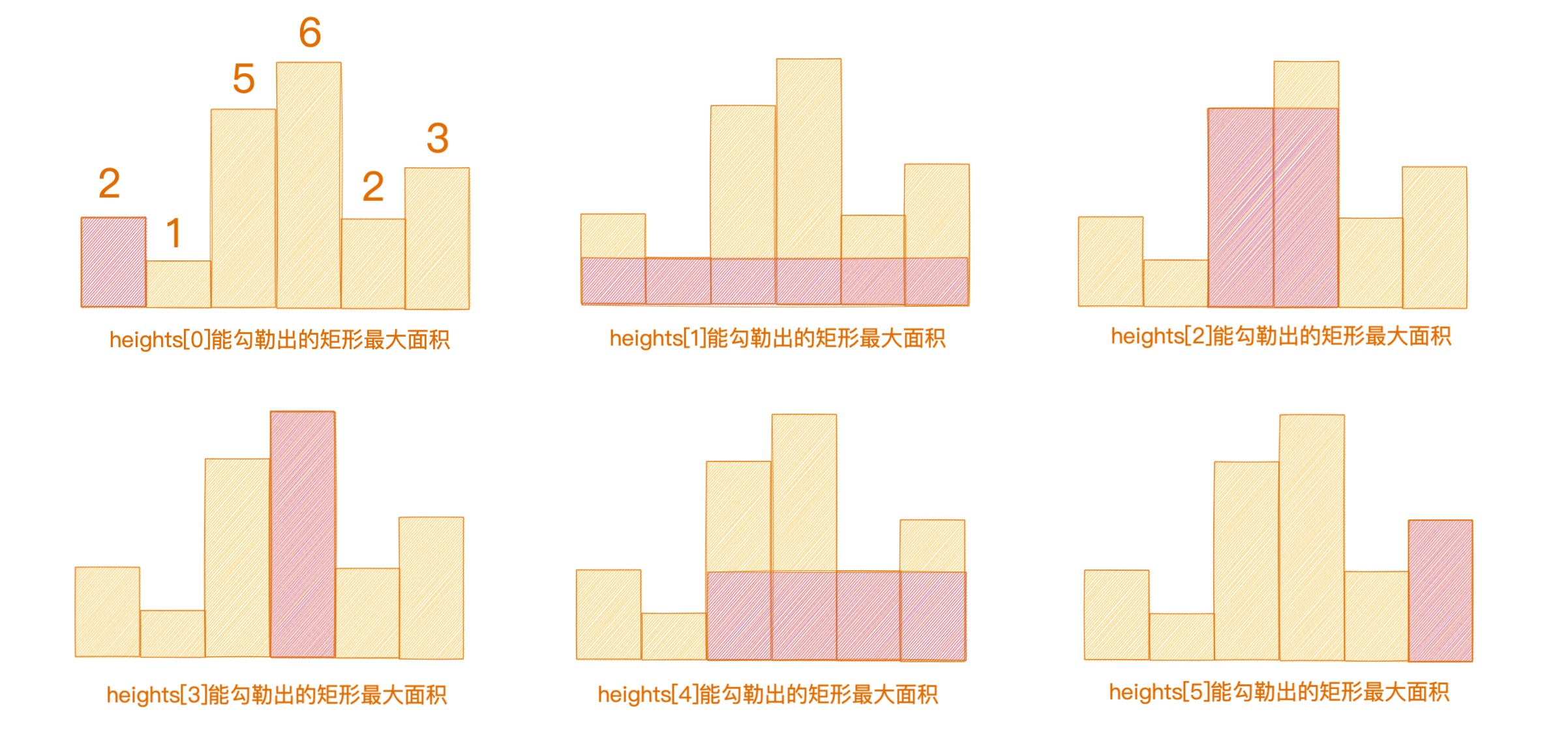
读题的第一遍,实际上就是要求在宽度为 1 的 n 个柱子能勾勒出来的矩形的最大面积。
这不就是个幼儿园的数学问题吗?
面积 = 底 * 高
撸它!
暴力法
方法一:双重循环遍历出所有的可能性,在遍历的过程中我们还可以求出最小的高度。
const largestRectangleArea = function(heights) {
let maxArea = 0
let len = heights.length
for (let i = 0; i < len; i++) {
let minHeight = heights[i]
for (let j = i; j < len; j++) {
minHeight = Math.min(minHeight, heights[j])
maxArea = Math.max(maxArea, minHeight * (j - i + 1))
}
}
}方法二:确定一根柱子后,分别向前后两个方向遍历。
const largestRectangleArea = function(heights) {
let maxArea = 0
let len = heights.length
for (let i = 0; i < len; i++) {
let left = i
let right = i
while (left >= 0 && heights[left] >= heights[i]) {
left--
}
while (right < len && heights[right] >= heights[i]) {
right++
}
maxArea = Math.max(maxArea, (right - left - 1) * heights[i])
}
return maxArea
}但是这两种方法的时间复杂度都是 O(n^2),空间复杂度是 O(1)。时间复杂度太高了,我们需要想办法进行优化。
使用单调递增栈
我们来思考一个问题,我们究竟想要求的最大面积是什么?
不妨拿起笔画画图,我这里帮你画好了,观察上图,便可以得出:
其实就是以 i 为中心,分别向左、向右找到第一个小于 heighs[i] 的两个边界,也就是以当前这根 i 柱子所能勾勒出的最大面积。
那么,我们为什么要借助单调递增栈这种数据结构呢?
单调递增,也就是我们可以通过 O(1) 的时间复杂度确定柱体 i 的左边界!
又是以空间换时间的套路!
如何确定右边界?
只需遍历一次柱体数组,将大于等于当前柱体的柱子们推入栈中,而当遍历到的柱子高度小于栈顶的柱子高度时,这时我们找到了右边界,可以将栈顶的柱子,弹出栈,来计算矩形面积了!
处理特殊边界情况?
引入前后边界,在柱体数组前后各放入一根高度为 0 的柱子。这样便无需考虑栈空以及栈中还有剩余柱子的情况啦!
ok,上代码!
const largestRectangleArea = function(heights) {
let maxArea = 0
let stack = []
heights.push(0)
heights.unshift(0)
// heights = [0, ...heights, 0] 你也可以这样写
for (let i = 0; i < heights.length; i++) {
while (stack.length > 0 && heights[stack[stack.length - 1]] > heights[i]) {
maxArea = Math.max(maxArea, heights[stack.pop()] * (i - stack[stack.length - 1] - 1))
}
stack.push(i)
}
return maxArea
}- 时间复杂度:O(n)
- 空间复杂度:O(n)